Introduction
While reading Computation: Finite and Infinite Machines by Marvin Minsky (originally published in 1967 but has remained largely relevant to this day) I ran across a problem which immediately sparked my interest. Here's an excerpt from the problem's description:
Consider a finite (but arbitrarily long) one-dimensional array of finite-state machines, all of which are alike except the ones at each end. The machines are called soldiers, and one of the end machines is called a General. The machines are synchronous, and the state of each machine at time \(t + 1\) depends on the states of itself and of its two neighbors at time \(t\). The problem is to specify the states and transitions of the soldiers in such a way that the General can cause them to go into one particular terminal state (i.e., they fire their guns) all at exactly the same time. At the beginning (i.e., \(t = 0\)) all the soldiers are assumed to be in a single state, the quiescent state. When the General undergoes the transition into the state labeled 'fire when ready', he does not take any initiative afterwards, and the rest is up to the soldiers. The signal can propagate down the line no faster than one soldier per unit of time, and their problem is how to get all coordinated and in rhythm.
A bit of theory
But what is a finite-state machine, anyway? It's an abstract machine, a mathematical model of computation. This automaton can be in exactly one of a finite number of states at any given time, and it can advance from one state to another in response to some external inputs. A single transition is solely contingent on the machine's current state and the input signal it receives while in that state.
Without going into further details, let's look at an example. (You can also take a look at this nice informal introduction by none other than Jeffrey Ullman.)
An example
Consider the old river crossing puzzle of a man with a wolf, a goat, and a cabbage. The man's rowboat has enough room only for himself and a single one of his companions. If left unattended together, the wolf would eat the goat, or the goat would eat the cabbage. The man's challenge is to carry himself and his companions to the far bank of the river, without the goat or the cabbage being eaten.
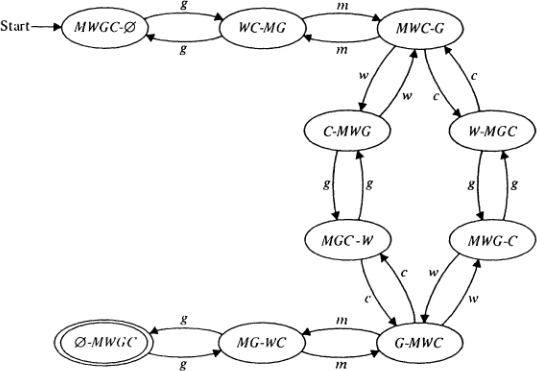
This puzzle can be modeled using a finite-state machine. Let's define the states. There are sixteen subsets of the man (\(M\)), the wolf (\(W\)), the goat (\(G\)), and the cabbage (\(C\)). Each state will correspond to the subset that is on the near bank of the river. States are labeled by hyphenated pairs, where the symbols to the left of the hyphen denote the subset on the near bank, and symbols to the right of the hyphen denote the subset on the far bank. Yet six of the states are dangerous, so we should never have reached them: \(M{\text -}WGC\), \(MW{\text -}GC\), \( MC{\text -}WG\), \(WG{\text -}MC\), \(GC{\text -}MW\), \(WGC{\text -}M\). What we're left with are ten valid states, one of which is our initial state, namely \(MWGC{\text -}\varnothing\). The "inputs" to the system are the actions the man takes. He may cross alone (\(m\)), with the wolf (\(w\)), the goat (\(g\)), or the cabbage (\(c\)). The final state is \(\varnothing{\text -}MWGC\), which means there's no one left on the near bank and everyone has crossed the river safely. Here's a transition diagram (this diagram is taken from Introduction to Automata Theory, Languages, and Computation (1st ed.) by John Hopcroft and Jeffrey Ullman):
A preliminary
Back to our original problem. Each of our soldiers, being a finite-state machine, has to have states and has to recognize inputs. Except for the quiescent and the final state, the rest of the states will be somewhat meaningless (non-semantic) in that they will only represent intermediate steps until the final state is hopefully reached. This is not to say that they will lack pattern, because such pattern is exactly the goal of our inquiry. This pattern will become even more apparent once we visualize the transitions. And what will be the inputs? Recall that "the state of each machine at time \(t + 1\) depends on the states of itself and of its two neighbors at time \(t\)". We already know that the state-to-state transition is a function of the machine's current state and the input it receives while being in that state. This means that the inputs to our soldier automata will be the states of its neighbors. For instance, if a soldier has on its left a soldier in state \(0\), and on its right a soldier in state \(1\), the input is going to be \(01\). Also recall that the problem allows for the General and the rightmost soldier to be slightly different, for they don't have two neighbors each, so their respective inputs are subject to the states of their one neighbor alone while we imagine their other (non-extant) neighbor to be in some predetermined, fixed state.
The number of states should be fixed and relatively small. In particular, the soldier with \(K\) states should work correctly regardless of the length \(n\) of the firing squad. Any solution to the problem requires at least \(2n - 2\) units of time from the General's order until the guns go off. It turns out that this minimal-time solution was found five years after the problem was originally proposed. But that wasn't the first solution found, and certainly not the most intuitive one. John McCarthy and Marvin Minsky came up with a solution first, and I was happy to notice that my solution was fairly similar to theirs. It's very intuitive and quite easily understood.
A solution
We divide and conquer. We send two signals down the line, one which propagates one soldier per time unit, and the other moving three times as slow. The first signal bounces off of the rightmost soldier and, on its way back, meets the second one in the middle of the firing squad. After that we recursively repeat the process in each of the smaller segments of the line until the segments simultaneously become small enough, and that's when the soldiers receive the decisive input to fire their guns - all at the same time. Here's a color-coded diagram representing the soldier automaton:
➩
➩
➩
➩
➩
➩
➩
➩
✱✱➩
✱✱➩
➩
➩
➩
➩
➩
➩
➩
✱➩
✱➩
➩
✱➩
✱➩
✱➩
✱➩
✱➩
✱➩
➩
➩
✱➩
✱➩
✱✱➩
✱✱➩
✱✱➩
✱✱➩
✱➩
✱➩
✱✱✱➩
Different colors stand for different states (✱ stands for any state). There are thirteen states in all. Each row of the diagram is akin to a separate rule which has three units resulting in a single one. The second of these units represents the soldier we're currently looking at, and the first and third represent soldiers to his left and right, respectively. The resluting unit's color represents the state the soldier we're looking at is going to advance to in the way we described in a preceding paragraph. If more than one rule from the diagram is applicable, the topmost of these gets precedence. I've purposefully led with this diagram, because it doesn't say much about the pattern we're after. One could still wonder how this construction brings us to a solution. It would be nice if we could visualize the very transitions that take place towards the coordination of soldiers.
Visualization
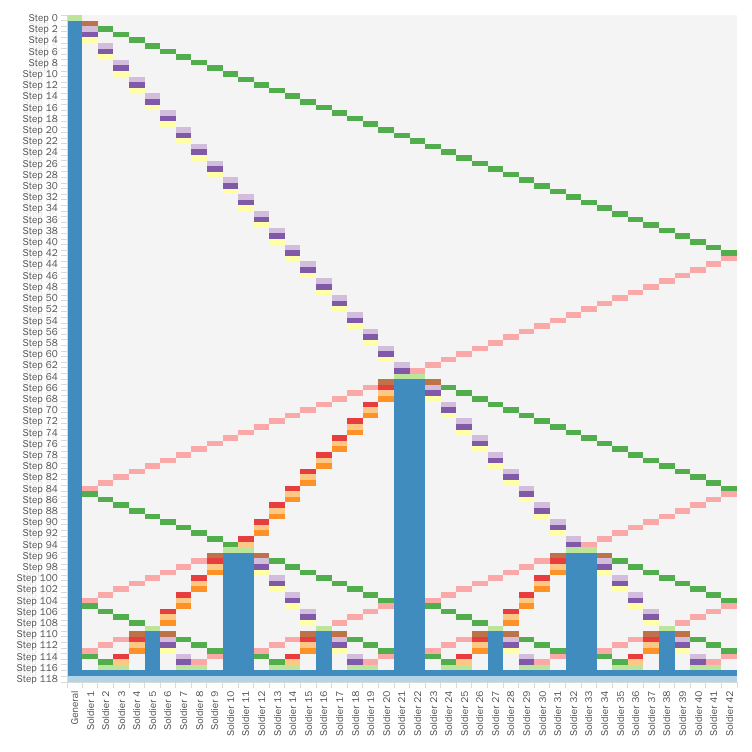
The best way to display such sequence of transitions over some discrete time is by using a matrix, or in data visualization parlance - a heat map. On the horizontal axis we will have singular soldiers, while the vertical axis will represent discrete slices of time. Each cell will then correspond to a state of a particular soldier at a particular time. Here we will use 42 soldiers besides the General:
Conclusion
As was requested, the solution works for any number of soldiers which is more readily seen now that we produced a visualization of its application to the \(n = 42\) case. All cases follow the same pattern taking no more than \(3n\) steps for all soldiers to reach the final state at the same time.
The study of cellular automata of automata theory is a fascinating field, not least because it has many applications in other fields of science which is outstandingly described and presented in A New Kind of Science by Stephen Wolfram, a book which I wholeheartedly recommend.
